Menentukan persanaan lingkaran jika diketahui titik pusat dan jari-jari.
Contoh:
Tentukan Persamaan lingkaran yang berpusat di (3, –2) dan berjari-jari 3?
Gambar lingkarannya seperti di bawah ini!
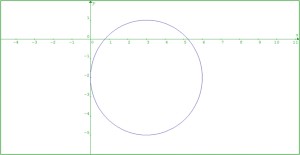
Dengan menggunakan rumus persamaan lingkaran yang berpusat di (a,b) maka didapatkan
(x – a)2 + (y – b)2 = r2
Diketahui dari soal, (a,b) = (3, –2)
Dan r = 3
Sehingga persamaan pun menjadi
(x – 3)2 + (y + 2)2 = 32
(x – 3)2 + (y + 2)2 = 9
Variasi soal lingkaran ini tidak terlalu banyak. Beberapa tipe soal akan diberikan cara penyelesaiannya.
Mencari persamaan lingkaran yang berpusat di (a,b) dan berjari-jari r. dapat dikerjakan dengan cara memasukkan langsung ke dalam rumus.
Menentukan persamaan lingkaran
0 komentar:
Posting Komentar
Jangan cuma baca, sampaikan kripik dan sarapan anda melalui komentar.